Constrained Reinforcement Learning using Distributional Representation for Trustworthy Quadrotor UAV Tracking Control

IEEE Transactions on Automation Science and Engineering

Yanran Wang*     David Boyle        

* Corresponding Author

Systems and Algorithms Lab, Imperial College London, United Kingdom.  
Paper arXiv Video Github



ConsDRED-SMPC - Practical implementation for challenging flight scenarios:

 

This implementation aims to address complex flight scenarios: dynamic (and unknown) constraint areas + unforeseen external forces + dense obstacles. VID-Fusion is used to measure external forces, such as aerodynamic effects.

Video


Motivation - Abstract

This work is motivated by challenges in training Reinforcement Learning (RL) for autonomous navigation in unmanned aerial vehicles, but its implications extend to other high-criticality applications in, for example, healthcare and financial services. The implementation of RL algorithm policies may exhibit various deficiencies, including:

a. opaque or unstable training due to the blackbox nature of deep neural networks; b. difficulty in reproducing RL outcomes; c. heightened costs associated with robustness investigation, e.g., hyperparameter tuning and generalization.

Abstract: Simultaneously accurate and reliable tracking control for quadrotors in complex dynamic environments is challenging. The chaotic nature of aerodynamics, derived from drag forces and moment variations, makes precise identification difficult. Consequently, many existing quadrotor tracking systems treat these aerodynamic effects as simple `disturbances' in conventional control approaches. We propose a novel and interpretable trajectory tracker integrating a distributional Reinforcement Learning (RL) disturbance estimator for unknown aerodynamic effects with a Stochastic Model Predictive Controller (SMPC). Specifically, the proposed estimator `Constrained Distributional REinforced-Disturbance-estimator' (ConsDRED) effectively identifies uncertainties between the true and estimated values of aerodynamic effects. Control parameterization employs simplified affine disturbance feedback to ensure convexity, which is seamlessly integrated with the SMPC. We theoretically guarantee that ConsDRED achieves an optimal global convergence rate, and sublinear rates if constraints are violated with certain error decreases as neural network dimensions increase. To demonstrate practicality, we show convergent training, in simulation and real-world experiments, and empirically verify that ConsDRED is less sensitive to hyperparameter settings compared with canonical constrained RL. Our system substantially improves accumulative tracking errors by at least 70%, compared with the recent art. Importantly, the proposed ConsDRED-SMPC framework balances the trade-off between pursuing high performance and obeying conservative constraints for practical implementations.

Method



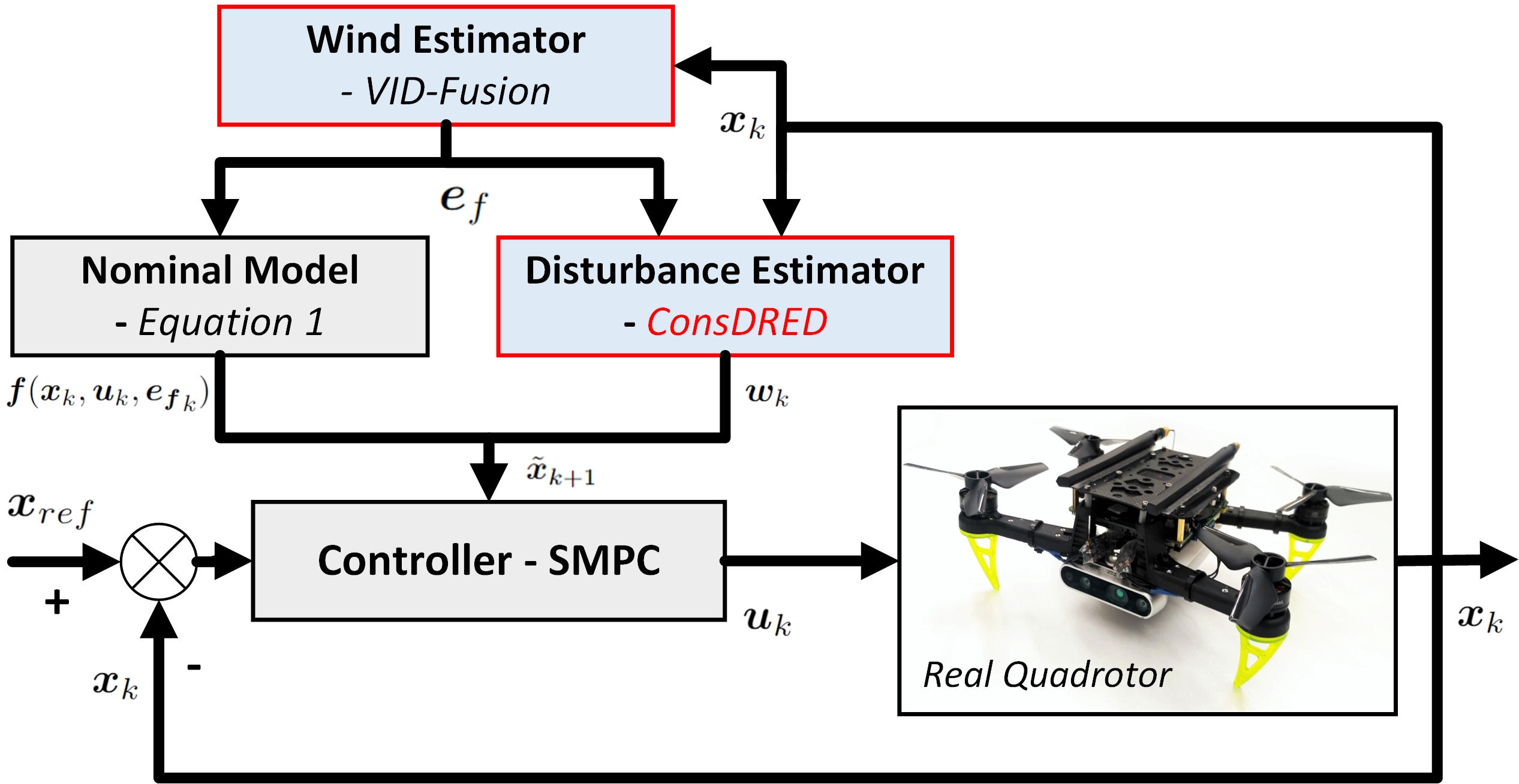
System overview of ConsDRED-SMPC:

We propose Constrained Distributional REinforced-Disturbance-estimation for Stochastic MPC (ConsDRED-SMPC), a systematic, trustworthy and feasible quadrotor trajectory tracking framework for use under high variance aerodynamic effects. To our best knowledge, this study represents the first attempt within the robot learning community to develop a trustworthy interpretation of an RL-based disturbance estimator through practical implementation. The details are as

(i) An aerodynamic Disturbance Estimator, i.e., ConsDRED, is proposed for aerodynamic disturbance estimation. This estimation relies on the wind estimation obtained from VID-Fusion.

(ii) A tracking controller, i.e., SMPC, a Simplified Affine Disturbance Feedback (SADF) is used for control parameterization in SMPC. Specifically, we use an Input-to-State Stability (ISS) property to imply stability and convergence of the tracker.

Experimental Results

(Baseline denotes the same setting hypermeters and environments integrated with ConsDRED-SMPC.)

 

Tracking Performance in Simulated Tasks

The flight task in the simulated scenario is to track the seven reference waypoints. In the external disturbance zone, the quadrotor system operates with the programmatic external forces, i.e., ${E}_{f,1}=[0.0, 3.0, 0.0]$ ($ms^{-2}$), ${E}_{f,2}=[-3.0, 3.0, 0.0]$ ($ms^{-2}$) and ${E}_{f,2}=[-4.0, 4.0, 0.0]$ ($ms^{-2}$), in the horizontal plane.

 

 

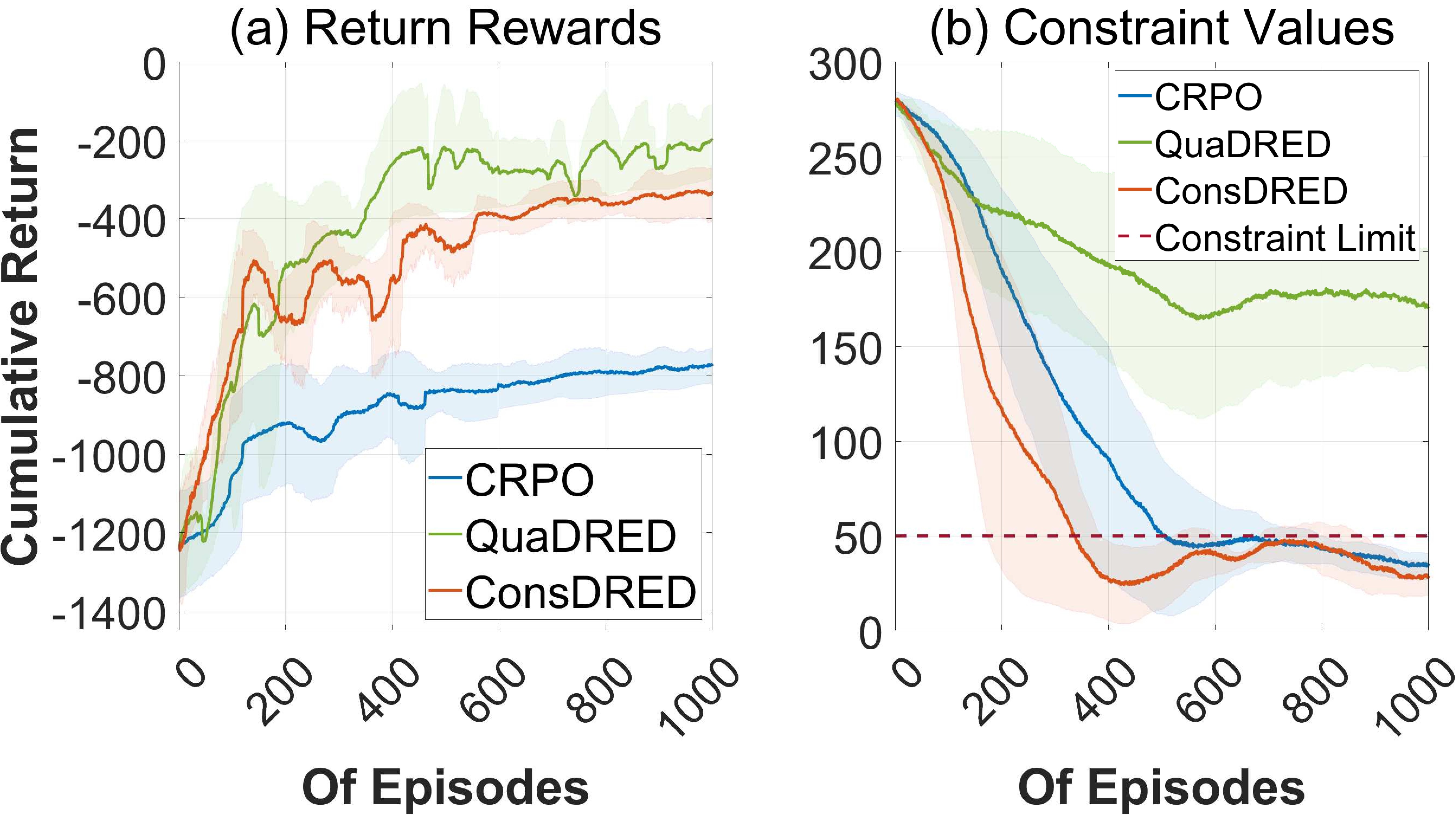
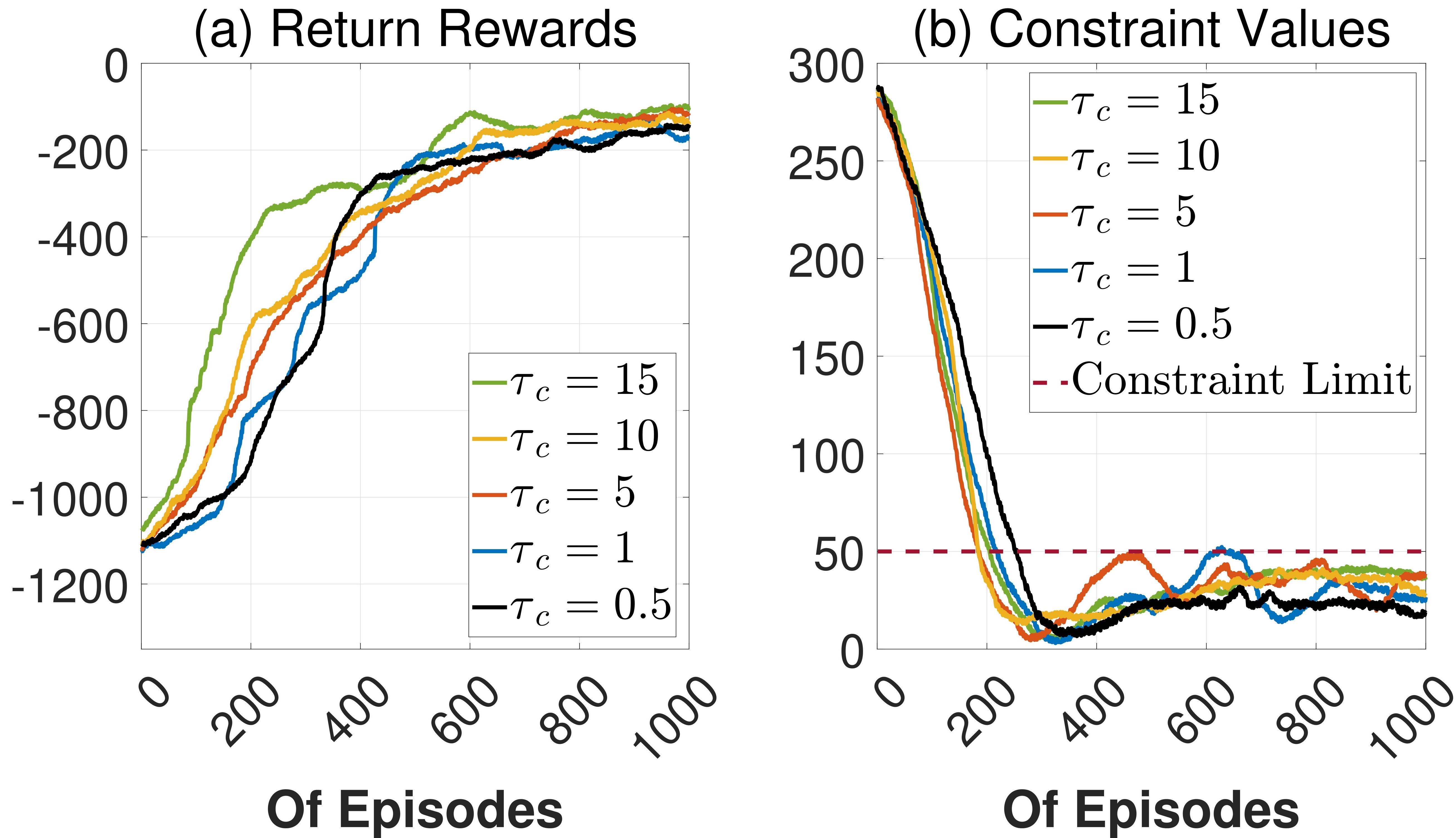
The learning curves and the robustness of the tolerance hyperparameter ${\tau}_{c}$ setting, in relation to the convergence process:

 

 

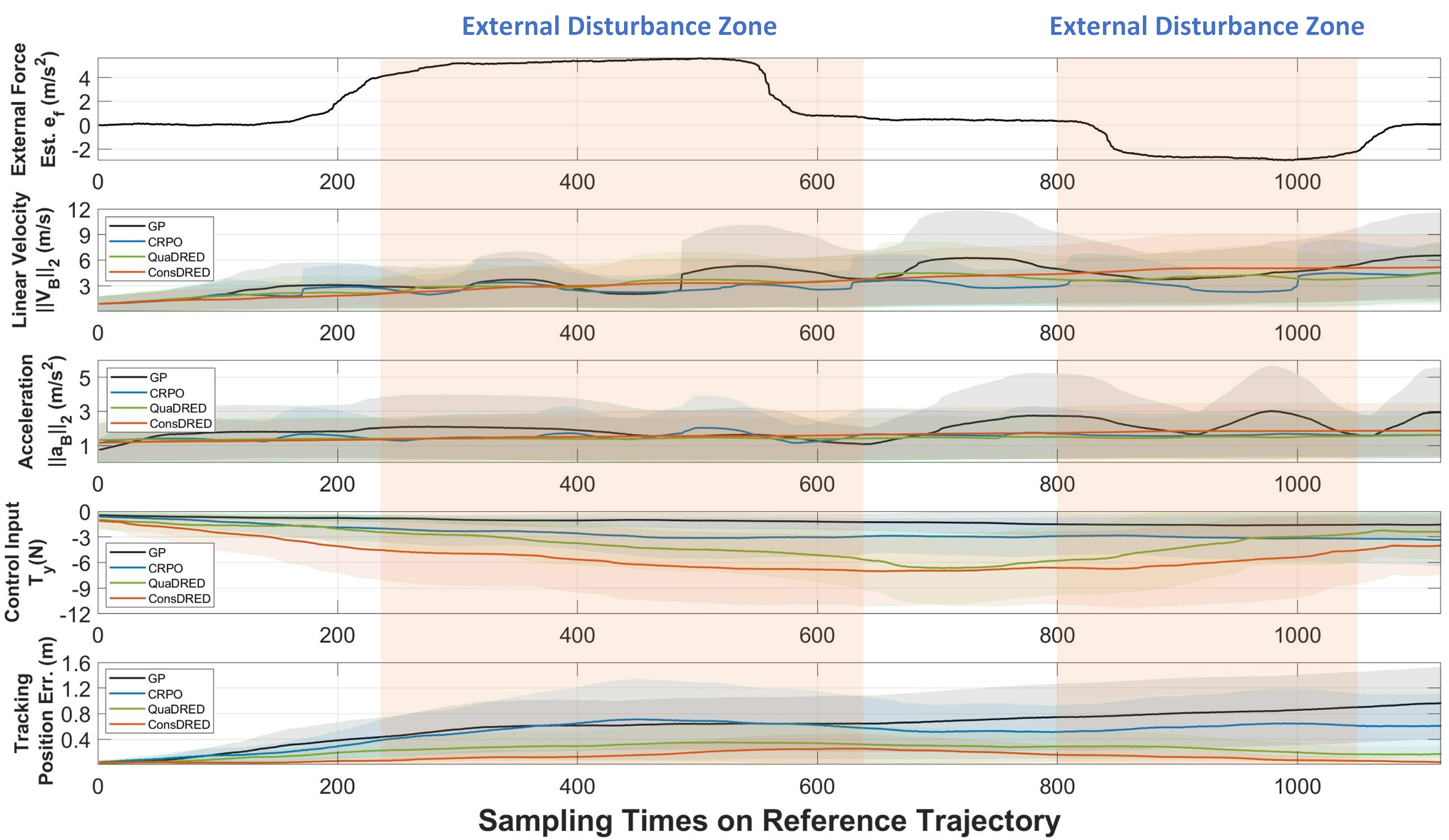
The simulation tracking performance is assessed with variance measurement: the external force estimation ${e}_{f}$($m/s^{2}$), linear velocity $\left \|{V}_{B}\right \|_2$, acceleration $\left \|{a}_{B}\right \|_2$, the control input $T_y$ (expressed in the body frame), and tracking position error ($m$). The X-axis unit corresponds to the number of sampling times, with 1100 sampling points evenly distributed along a trajectory. The results from a single run are depicted in the figure below.

 

 

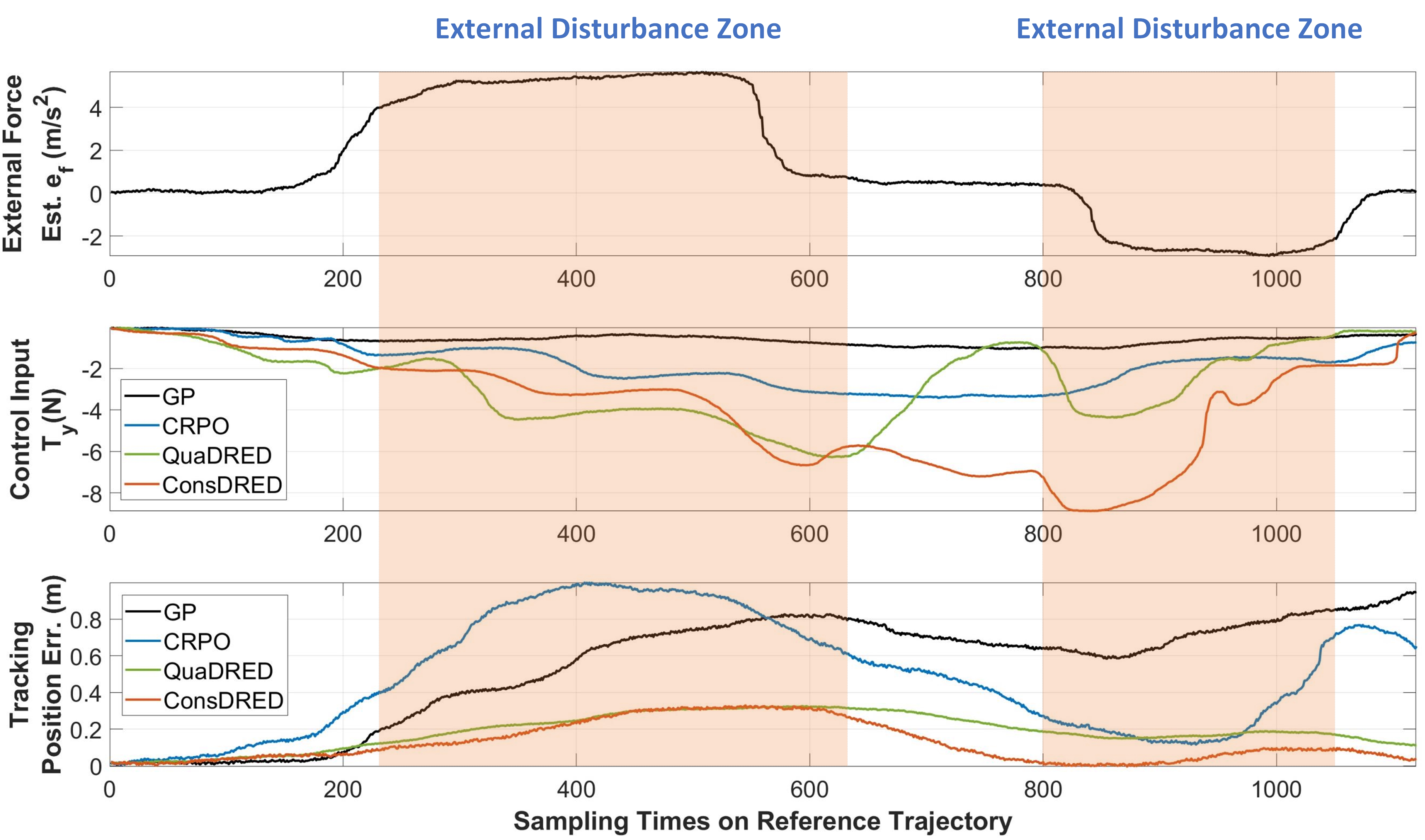
The simulation results from one run include the external force estimation ${e}_{f}$, the control input $T_y$ (expressed in the body frame), and tracking position error $(m)$.

 

Comparative Performance in Real-world Tasks

We use our ConsDRED-SMPC as the tracking controller for a quadrotor. The aim is to evaluate two properties of the trained ConsDRED: (i) convergence quality in the real physical experiments, and (ii) generalization capability under unprecedented external forces.

 

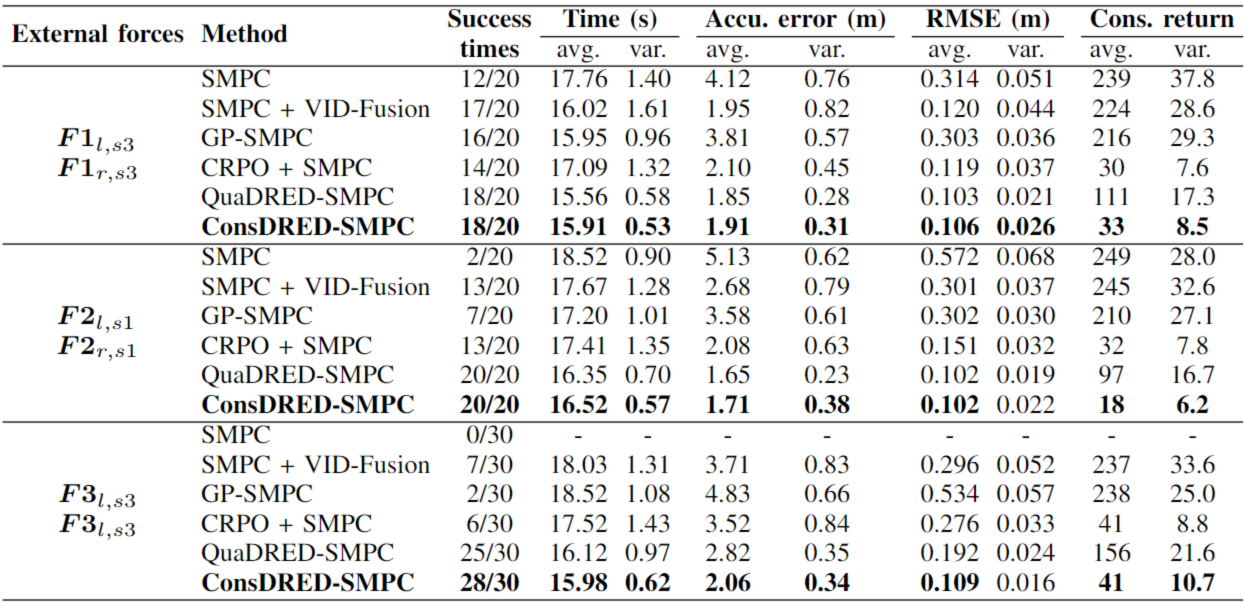
Real-world trajectory tracking under variable external forces: the scenario 1 and 3 are applied for tracking performance evaluation. Let the external forces from the left / right fans in scenario 1 / 3 be ${F1}_{l,s3}=2.5$ ($ms^{-1}$), ${F1}_{r,s3}=1.5$ ($ms^{-1}$); ${F2}_{l,s1}=3.5$ ($ms^{-1}$), ${F2}_{r,s1}=2.5$ ($ms^{-1}$); and ${F3}_{l,s3}=3.5$ ($ms^{-1}$), ${F3}_{r,s3}=2.5$ ($ms^{-1}$).

 

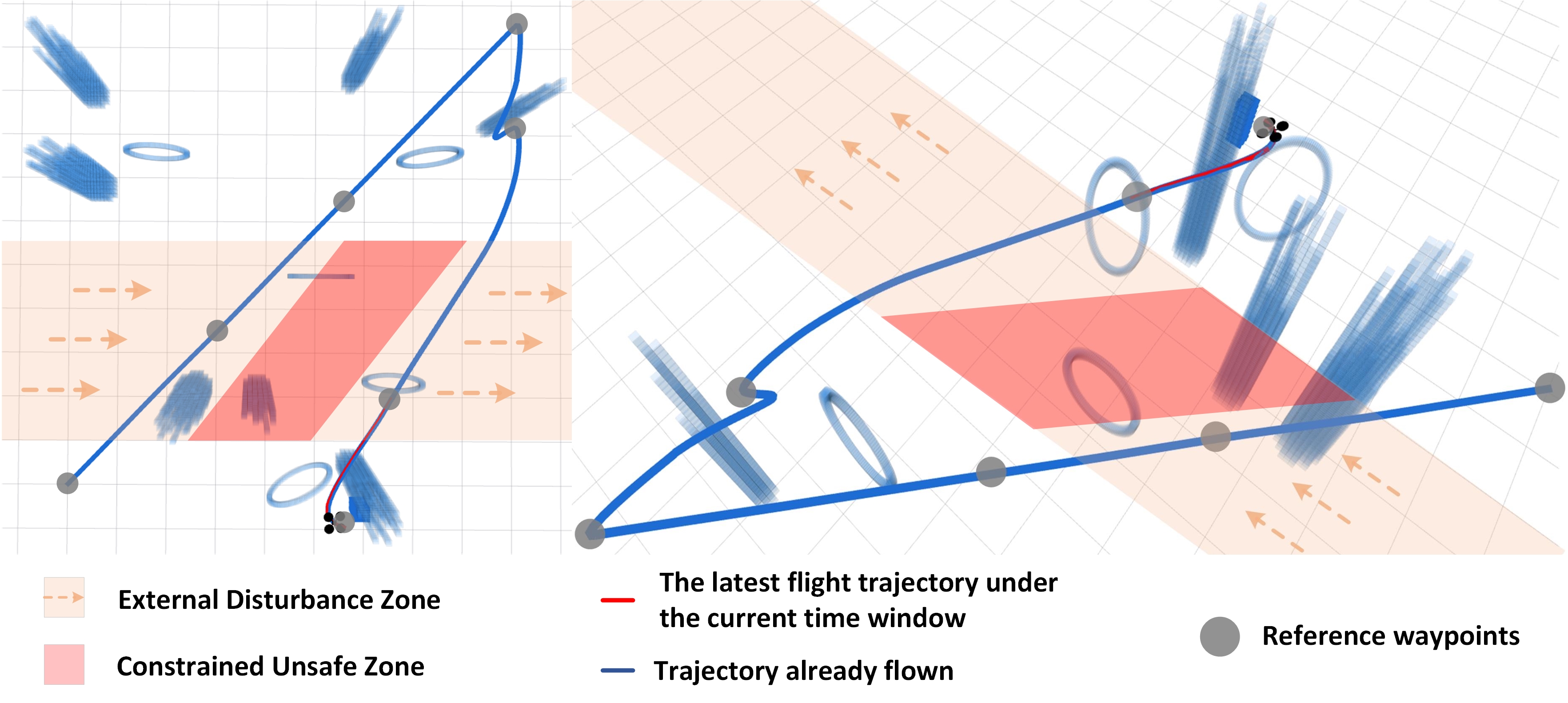
Real-world Scenario 1: tracking trajectories under external forces without obstacles, where the agent learns the aerodynamic effects like turbulent effects caused by dynamic rotor–rotor and rotor-airframe interactions in Flight Task 1-2.

 

Real-world Scenario 2: tracking trajectories around the static (no external forces) but dense obstacles, where the agent learns the turbulent effects from rotor-obstacle interactions in Flight Task 3-4.

 

Real-world Scenario 3: tracking trajectories under external forces around dense obstacles, where the agent learns the comprehensive aerodynamic effects from a combination of the dynamic rotor–rotor, rotor-airframe, and rotor-obstacle interactions in Flight Task 5-6.

 

The influence of ConsDRED becomes even more evident in this real-world tracking experiments. The contribution of ConsDRED rises significantly from $6.7\%$ to $57\%$ as the wind intensifies, transitioning from ${F1}_{l,s3}=2.5$ ($ms^{-1}$), ${F1}_{r,s3}=1.5$ ($ms^{-1}$) to ${F2}_{l,s1}=3.5$ ($ms^{-1}$), ${F2}_{r,s1}=2.5$ ($ms^{-1}$). For details, please refer to the table below.

 

BibTeX

@article{wang2024constrained,
      title={Constrained Reinforcement Learning Using Distributional Representation for Trustworthy Quadrotor UAV Tracking Control},
      author={Wang, Yanran and Boyle, David},
      journal={IEEE Transactions on Automation Science and Engineering},
      year={2024},
      publisher={IEEE},
      pages={1-18},
      doi={10.1109/TASE.2024.3432405}
    }

Acknowledgements

This work was supported in part by the National Science Foundation (NSF)-UK Research and Innovation (UKRI) under Grant NE/T011467/1 and in part by the Engineering and Physical Sciences Research Council under Grant EP/X040518/1.